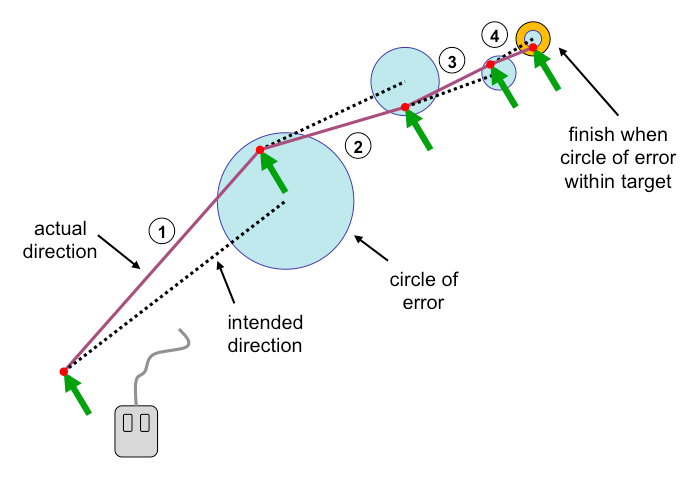
Figure 1. step-wise movement towards target
Human-Computer Interaction 3e Dix, Finlay, Abowd, Beale
Most treatments of Fitts' Law say WHAT is true, but not WHY. However, if one understands why it is easier to predict where it will hold and where fail. Whilst Fitts' original paper uses an analogy with Shannon and Weaver's information theory, it does little more than postulate some neurological information rate.
In fact it is easier to understand Fitts' Law if one considers the control task of hand-eye coordination. This is an interaction - one moves the mouse (or other pointer), the eyes see the movement, you correct etc. This all happens in a fraction of a second.
Timing is critical as the delay between seeing something, the processing to be done in your brain and the signal to get down your arm to your muscles is between 150 and 200 milliseconds. Your arms moves a long way in that time, typically 70-90% of the way to the target. This is rather like controlling one of those Mars robots where the transmission delay can be 20 minutes or even more when Mars is further away. You could very very slowly move it inch by inch, or you could work out approximately where a speed and direction would take it in 20 minutes and send it trundling off.
The human process is faster, but similar in nature.
(In fact, for the Mars Rover the times are so long that the vehicle has its own autonomous control as well, this is rather like the fact that your hand pulls back from heat before the signals ever getting to your brain.)
Imagine we are writing the control circuitry for the human hand-eye pointing task.
Let's look at a basic motor control cycle:
This whole cycle has a minimum time associated with it due to the delays in processing in your brain, sending signals to the arms etc.
Let's assume two further things;
Now as a continuous process this is hard to imagine, especially because of the delays ... it is like a general commanding an army in the days before radio, you only ever know where your soldiers were several days ago.
However, if instead we imagine this more as a series of discrete movements it is easier to imagine. Each movement corresponds to the hand-eye period.
Whilst this is a bit of a simplification it gives the general idea quite well, and indeed corresponds very closely to the observed behaviour for certain pointing devices. For others, in particular mouse movement, the process is not move-stop-view-plan, but more one of constant correction, but the time for the correction cycle is similar.
Figure 1 shows a discrete steps through 4 cycles of sensing and movement. The diagram shows how the movements in each step get gradually smaller as the target gets closer.
Because of the processing delay the shorter paths cannot be executed faster than the minimum delay. So it is reasonable to assume (c) that the brain tells the muscles to move slower and slower as the target gets closer. That is the time for each movement constant, not dependent on the distance moved.
Finally, because the errors are proportional to distance, the movements get smaller geometrically.

Figure 1. step-wise movement towards target
So we have a sequence of moves, each of which reduces the distance to the target geometrically and each of which takes the same time. When remaining distance is such that the error circle of the remaining movement is less than the size of the target then we can actually move and get inside the target.
You can do a little experiment to see what this is like.
I find I can hit toolbar-sized icons in about 3 steps and things like the window open and close boxes in no more than 4.
You may be surprised too at how accurate you are on the first movement.
I also find I tend to always undershoot - hence Figure 1 is drawn like that, although the calculations below do not depend on that. In fact it is reasonable that we subconsciously tend to undershoot in positioning tasks as real world positioning is often to grab something. If you over shoot you will hurt your hand, or knock over the thing you are trying to grab.
Although the analogy with Shannon and Weaver's information theory is not sufficient in itself to explain Fitts' Law, the fact that the two formulae correspond so closely is no accident.
Think of the "infinite" Fitts' task of trying to hit an exact (size zero) target. Of course you could never do this, but it is really just to give the flavour. The pointing task could be thought of as trying to communicate the location from the eye tot he mouse pointer ... but the channel (the visual-muscle system) has errors and hence is noisy. The noise level is related to the distance moved and hence gives an maximum rate on the amount of information it can carry.
For the finite Fitts' task we only care about positioning to an accuracy of S and hence we only need log(D/S) bits of information to be "communicated".
From the cybernetic description we can also see that the assumptions allow us to see the limits where Fitts' Law will fail.
One of the critical human abilities is to be able to tell your muscles where to move and to be able to predict where this will take the pointer. In the case of indirect pointing through a mouse, joystick or other devices, this means our brains have to 'understand' (in a tacit sense) the acceleration and other non-linear mappings between movement and location.
It is in fact quite amazing that our brains are able to learn these complex mappings (see Alan's cyborg driving essay for an explanation why!). However, it takes time and practice. This is why (and usually not stated) Fitts' Law depends on 'over learnt' behaviour, that is use of a device that is so practised that the user has attained peak performance.
Not only does the brain need to know where the expected location of the pointer will be after one hand-eye cycle, but also, to avoid overshoot, how accurate that estimate is. So, for a device with some inaccuracy or noise in addition to those of your muscles, your brain needs to be able to 'learn' this level of inaccuracy to be able to assess how far short of the target to aim.
This is why menus at the top or bottom of the screen help, the overshoot is less important so your brain can afford to aim to hit in one movement, rather than fall short, of the target.
Any delay in the device adds to the total time of the hand-eye coordination loop. This gives rise to a slow down in the whole process and the 'B' figure gets larger by a factor of (τh + τd) / τh, where τh is the hand-eye coordination time and τd is the device delay. This effect has been observed in experiments.
The logarithmic number of steps to the target is also dependent on the maximum speed of the device allowing a virtually complete movement to target within one hand-eye cycle. If this is not the case then a series of smaller steps will need to be taken and a different timing behaviour would be observed. For a screen size of around 1000 pixels, this means the device must be able to support movement speeds of the order of 5000 pixels per second.
Similarly at the lower end, the minimum (non stationary) movement speed must be such that the target is not missed entirely within one hand eye cycle. For example, if the target is 10 pixels across, the minimum speed needs to be around 50 pixels per second.
In informal experiment with game controllers Kiel Gilleade found that most of the small thumb joystocks on these did not obey Fitts' Law because they broke one or more of the constraints above. This is not to say they are not good controllers, just they are not Fitts' Law ones. In fact Kiel observes that real gamers simply push the controllers to max all the time anyway!
See also CHI papers on Fitts' Law of path following and the way Fitts' law constant changes as the movement changed to different muscle groups (arm vs. wrist vs. finger movement).
Mathematically let the distance to the target at each stage be Di and the distance moved di:
D0 = D - the initial distance
di = λ Di - where λ is some empirical constant
Di+1 = (1-λ) Di
so:
Di = (1-λ)i D
The error circle is radius ri:
ri = σ di - where σ is some empirical constant
ri = σ λ (1-λ)i D
The process stops after n steps when the radius rn is less than the target size S:
σ λ (1-λ)n D < S
So n is approximately:
-log ( σ λ D / S ) / log ( 1-λ )
Each step takes a fixed time τ, and there will be some initial time for the brain to "get started", say α. So the total time T is given by:
T = α + τ n
= α + τ ( -log ( σ λ D / S ) / log ( 1-λ ) )
T = A + B log ( D / S )
where
A = α - τ log ( σ λ ) / log ( 1-λ )
B = - τ / log ( 1-λ )
N.B. log(1-λ) is negative so B is positive
Alan Dix © 2003,2005