Figure 1. pull-out hierarchical menu
Human-Computer Interaction 3e Dix, Finlay, Abowd, Beale
Hierarchical menus are ubiquitous in user interfaces. In desktop applications these are usually pull out menus. In web applications this is often in the form of screen-based selections, for example, in an online catalogue one may initially select from a number of top-level categories in the store (say choosing 'furniture'), then on the next page one selects a subcategory (say 'dining tables') and so on.
In such a menu the number of selections at each level is called the breadth of the menu and the number of levels is called the depth. For example, the menu in Figure 1 has depth 3, with breadth 11 at the first level, breadth 7 at the next level and breadth 10 at the lowest level. As a designer of such menus, one often has the problem of deciding how many choices to put at each level. For example, in Figure 1, the top level has two dividers separating the menu into three parts - why didn't the designer give each part a menu and add another level with three initial selections at the top level? This would have made a deeper, and narrower (lees broad) menu. Which is better?
In Chapter 5, we note that Millers 7+/-2 is often used in situations where it does not apply, and in particular to the choice of menu breadth. It is not unusual to see suggestions that the breadth should not exceed 7+/-2 items.
To see why this is not appropriate, think of the steps that happen as you navigate a menu:
1. visually find the necessary menu item
2. select the item (with mouse or finger depending on the device)
3. wait for the system to show the next level of the menu
4. start again at 1 until you get to the bottom of the hierarchy
Steps 1 and 2 will both depend on the breadth of the menu.
For a desktop application the time in step 3 is usually negligible, but for web-based applications this often requires a fresh page to be loaded or an AJAX-based call to retrieve more information from the web server. Either way, it is normally independent of the menu breadth
Finally at (4) the number of times we do steps 1 to 3 is given by the depth of the menu.
Note that when you scan a menu at step 1, you do NOT have to remember the items - they are there in front of you. For simple menus, such as alphabetic list, all one has to do is scan until you notice the right position. At worst, for complex menu choices, you may need to keep track of the most likely option so far and then go back to it. Either way memory is unlikely to be the limiting factor (although there is some evidence that in certain cases better working memory does help).
In order to estimate the actual time, we assume the menu is uniform in its depth and breadth (every sub-menu with the same number of choices, and the same number of levels down every branch). We will call the breadth B and the depth D. Of course, this is rarely the case , but we can use it to give an indication of what to expect in more realistic cases ... and in fact experiments on menu selection almost always use this kind of very uniform menu.
Note that the breadth and depth are not independent as we normally have a fixed number of total items, say N, that we wish to select between. N, D and B are related by:
N = B D
or equivalently:
D = log(N) / log(B)
Basically, of the menu is broad we need less levels to access the same number of items.
Looking back to steps 1-4, we can say that the total section time is:
D x ( choice time + selection time + system response time )
where the three terms correspond to steps 1, 2 and 3 and the factor D is because we need to do the step for each level of the menu hierarchy.
The last of these, system response time, we have already noted is usually independent of the choice of breadth and depth. Call it RT, a fixed number.
The selection time at step 2 is usually a Fitts' Law task (see Chapter 1, page 27) and the average distance travelled will grow with the breadth of the menu, but the size of target is basically the size of the words (or icons) used in the menu, so will be constant. Recall that in Fitts' Law selection time is proportional to the logarithm of distance/size. This means that the selection time, call it ST, ends up increasing with log(B):
ST = a + b log(B)
The time taken for step 1, is the most complicated and also depends on complexity of the menu choice.
If the menu is completely unseen and unordered (or of the user does not recognise or understand the order), then the user has to visually scan each item one by one. In this case, the choice time, call it CT, is proportional to B:
CT = c x B
However, if the menu is ordered or well known and the user can scan it more efficiently (maybe skip their eye to the middle and move up and down form there), then Hick's Law (also known as Hick-Hyman Law) is more appropriate. Hick's Law says that the time it takes to choose between n choices is proportional to log(n). In this case at each level there are B choices, so this suggests that:
CT = c x log(B)
In the first case, the overall time is:
total time = D ( c x B + a + b log(B) + RT)
Recalling that D = log(N)/log(B), this is:
( log(N) / log(B) ) x ( c x B + a + b log(B) + RT)
= log(N) x ( c x B / log(B) + b + (a+RT) / log(B) )
The first of these terms grows as B gets bigger and the second gets smaller as B gets bigger, so there is an optimal menu breadth. However, for web-based systems where the system response time may be several seconds, and with reasonable estimates for the constants in Fitts' Law and choice time, the optimum breadth is around 60!
In fact, when Larson and Czerwinski examined menu structures they found that broad menus, with 16 and 64 items per level performed better and were preferred by users compared with narrower ones with breadths of 4 or 8.
In the second case, using Hick's Law to predict choice time we get:
total time = D ( c x log(B) + a + b log(B) + RT)
Notice that all the terms inside the brackets, which is the time per selection are either constant or involve the logarithm of the breadth. Early experiments by Landauer and Nachbar showed just this, with selection time increasing with the logarithm of the breadth.
If we again take D = log(N) / log(B), we get:
( log(N) / log(B) ) x ( c x log(B) + a + b log(B) + RT)
= log(N) x ( (c +b) + (a +RT) / log(B))
This always gets smaller as the breadth increases, suggesting that the best menus are the widest one ... with no limits!
So in the first case (sequential scan of menu items) there may be an optimum size, but it is quite large, whereas where the latter holds (Hick's Law), the bigger the better!
In fact, at some stage the screen gets full, or so cluttered it is hard to read, so there are always limits, but in all cases the best breadth tends to be a lot bigger than 7+/-2!
As noted while theoretically very broad menus may be best, in practice other factors come into play. In particular, the use of Hick's Law or even sequential scan time assumes 'all things being equal', but in fact some categorisations make more sense than others.
For example, consider again the menu in Figure 1 (expanded in Figure 2). We asked why it has not had an extra level added corresponding to the three sections. Not only does the analysis above suggest that this would be counterproductive in making the menu deeper and narrower, but also it is not at all obvious what to call the three resulting sections. If they are not named clearly and unambiguously then users will get confused, take longer to choose the right options and make more mistakes.
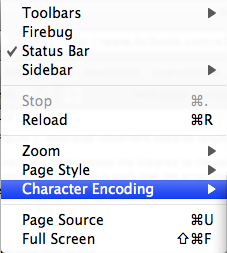
Figure 2. menu sections
Landauer and Nachbar emphasise this using the states of USA as an example. It would usually be faster to simply show all 50 states than to try to divide them into three categories of 15 or so each or even worse 25 categories of pairs of states.
However, Figure 1 and 2 show a heuristic that can help in practice, namely to actually use category divisions within a single menu level. The division into section can help the user orient themselves to the right part of the menu. Similarly, in the case of an online catalogue, one might organise the top-level page into portions labelled 'furniture', 'garden', 'home decoration', but then within the furniture portion of the screen list all the types of furniture: 'dining tables', 'coffee tables', 'stools', 'sofas', etc.
This technique effectively 'flattens' several levels of a deeper narrower structure on the screen so that the user is using very fast visual scan, rather than much slower selection of sub-levels. In terms of the different parts above step 1, the choice time (step 1) is favoured, but the use of structure ensures that it becomes a Hick's Law not a sequential search task.
In fact, some studies have measured subject's short-term memory capability, and used this to test whether better memories lead to faster selection times. Larson and Czerwinski found that when faced with very broad menus, those with better short-term memory capacity performed slightly faster than those without. This is maybe because, for a very large menu, the user does need to keep track of the best choices so far. However, while memory capacity made a difference between subjects, all subjects were still better with the broader shallower menus - breadth is still best!
For very large hierarchies, or complex web navigation structures in general, in fact keeping track of where one is in the hierarchy depth is more likely to be a strain on memory than scanning the list of items being displayed. That is depth is the memory limit.
Alan Dix © 2010