EXERCISE 17.1
Using the model-oriented approach with
the example graphics program described in Section
17.2.3, specify the move operation as a schema which
acts on the currently selected objects. Is the operation
you have defined cumulative (two successive moves
can be done as one move which is the sum of the other
two) or is it 'forgetful?' Discuss the implications
of the framing problem in your definition.
answer
Students may not have a great familiarity
with the Z notation used in this textbook, especially
if they do not have a computer science background
which emphasizes formal specification. Nevertheless,
we will provide a model answer to this exercise in
the Z notation and leave it to the instructor to decide
whether an alternative language can be used to express
the same ideas.
To accommodate the specification of
the move operation, we will first need a function
which allows us to add two coordinate points together.
We just provide the declaration of this function here.
| _ + _: Point  Point Point  Point Point
The motivation for this function is
so that we can define a move operation with a single
argument, called delta?
below, which will specify how far to move the centres
of every selected shape. This approach, using relative
movements, will allow for two consecutive moves to
be defined with the overall movement being the sum
of the individual moves. Another approach (which would
be quite cumbersome to define for a set of selected
objects) would be to specify the move operation as
an absolute operation, the argument(s) to the move
explicitly indicating the new value for the centre(s)
of each selected shape. This operation definition
would not be cumulative.
Initially, we might want to define the
move operation simply to update the centre position
of all selected shapes.
___Move___________________________________________________________
| State
| State'
| delta? : Point
|____________________
|  id : selected id : selected  shapes'(id).centre = shapes(id).centre + delta?
|________________________________________________________________________ shapes'(id).centre = shapes(id).centre + delta?
|________________________________________________________________________
There are a number of details in this defined operation
which are left (dangerously) open to interpretation.
Many of these are framing conditions on the Move
operation. For example, what happens to shapes which
are not selected? The normal intuition on this operation
would be that they stay put, but the above definition
actually allows them to change in any way - including
the possibility of disappearing altogether. To ensure
that unselected objects stay the same as they were
before the operation, we would have to add a predicate
to the definition.
___Move___________________________________________________________
| State
| State'
| delta? : Point
|____________________
|  id : selected id : selected  shapes'(id).centre = shapes(id).centre + delta?
| shapes'(id).centre = shapes(id).centre + delta?
|  id : (dom shapes - selected) id : (dom shapes - selected)  shapes'(id) = shapes(id)
|________________________________________________________________________ shapes'(id) = shapes(id)
|________________________________________________________________________
We also need to explicitly state that no new shapes
are introduced into the system, i.e., that the domain
of shapes remains the same.
___Move___________________________________________________________
| State
| State'
| delta? : Point
|____________________
|  id : selected id : selected  shapes'(id).centre = shapes(id).centre + delta?
| shapes'(id).centre = shapes(id).centre + delta?
|  id : (dom shapes - selected) id : (dom shapes - selected)  shapes'(id) = shapes(id).centre
| dom shapes' = dom shapes
|________________________________________________________________________ shapes'(id) = shapes(id).centre
| dom shapes' = dom shapes
|________________________________________________________________________
For those familiar with Z, it is possible to collapse
the last three predicates in the above schema to one
predicate using functional overriding from the basic
Z mathematical toolkit (see Spivey [328]).
Another framing issue which has impact on the interactive
style of this graphics system is specifying what happens
to the selected set of shapes after the move operation.
Our current definition says nothing about this. Two
clear options are whether the set of selected shapes
remains the same or becomes the empty set (no selected
objects). For reasons of compositionality (for defining
consecutive move operations or consecutive operations
targeted at the same set of shapes) we choose the
former option, and specify this below.
___Move___________________________________________________________
| State
| State'
| delta? : Point
|____________________
|  id : selected id : selected  shapes'(id).centre = shapes(id).centre + delta?
| shapes'(id).centre = shapes(id).centre + delta?
|  id : (dom shapes - selected) id : (dom shapes - selected)  shapes'(id) = shapes(id)
| dom shapes' = dom shapes
| selected' = selected
|________________________________________________________________________ shapes'(id) = shapes(id)
| dom shapes' = dom shapes
| selected' = selected
|________________________________________________________________________
[Note: Experienced Z users would probably
choose the functional overriding operator ( )
to more concisely express the first three predicates
above.] )
to more concisely express the first three predicates
above.]
EXERCISE 17.2
Write a similar schema for
RESIZE. It should have the
following informal semantics. The width and height attributes
are of the shapes bounding box. The resize operation
should make one corner of the bounding box be at the
current mouse position (supplied as the argument current_pos?).
Hint: the width of a box is twice the difference
between the x coordinate of the centre and the x coordinate
of any corner:
wid = 2  | centre.x - corner.x | | centre.x - corner.x |
answer
Strictly speaking, there are some errors in the
Z usage for the hint in this exercise. The type Point
is not a schema type, and so it is not meaningful
to use schema selection, as in expressions like centre.x
and corner.x. The alert
Z student should pick up on this error. However, the
spirit of the hint is still valid. To make things
legal in Z, we can change the declaration of Point
as follows:
___Point____________________________________________________________
| x,y : 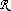 |__________________________________________________________________________
|__________________________________________________________________________
To best specify this resizing operation, we will
require to explicitly model the bounding box of a
shape. We introduce a type, called BoundingBox
which will represent the corners of the surrounding
box which defines the extent of a shape. In fact,
in Figure 17.1, we have drawn the bounding box for
the circle but we have not made that information explicit
in the specification in the text of this chapter.
We omit details in this sample answer on 'rectangular'
constraints for the corners of the bounding box (e.g.,
that upper left and right corners have the same y-coordinate
values but the x-coordinate of the upper left corner
is strictly less than the x-coordinate of the upper
right corner, etc.)
___BoundingBox______________________________________________________
| upperleft, upperright,
| lowerleft, lowerright : Point
|___________________________________________
| upperleft.x  upperright.x
| upperleft.y = upperright.y
|
| ...
|__________________________________________________________________________ upperright.x
| upperleft.y = upperright.y
|
| ...
|__________________________________________________________________________
We can add the bounding box as information known
about shapes, by extending the definition of Shape.
A constraint on the bounding box, motivated by the
hint to this exercise, is that its width and height
are the same as the width and height of the shape.
In addition, the centre coordinates are related to
the width and height. Note below that we use the names
height and width
in the definition of Shape
to increase its readability.
___Shape______________________________________________________
| type : Shape_type
| width : 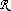 | height :
| height : 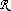 | centre : Point
| bb : BoundingBox
|___________________________________________
| width = 2
| centre : Point
| bb : BoundingBox
|___________________________________________
| width = 2  (centre.x - bb.upperleft.x)
| height = 2 (centre.x - bb.upperleft.x)
| height = 2  (centre.y - bb.upperleft.y)
| width = (bb.upperleft.x - bb.upperright.x)
| height = (bb.upperleft.y - bb.lowerleft.y)
|__________________________________________________________________________ (centre.y - bb.upperleft.y)
| width = (bb.upperleft.x - bb.upperright.x)
| height = (bb.upperleft.y - bb.lowerleft.y)
|__________________________________________________________________________
Resizing can be viewed as changing the size of the
bounding box. At a relatively abstract level, we can
simply specify the resizing operation with a single
argument indicating the new bounding box for the selected
shape. A precondition for the operation is that there
is only one selected shape.
___Resize______________________________________________________
| State
| State'
| newbb? : BoundingBox
|___________________________________________
| #selected = 1
|  id : selected id : selected  shapes'(id).bb = newbb?
| forallid : (dom shapes - selected) shapes'(id).bb = newbb?
| forallid : (dom shapes - selected)  shapes'(id) = shapes(id)
| dom shapes' = dom shapes
| selected' = selected
|__________________________________________________________________________ shapes'(id) = shapes(id)
| dom shapes' = dom shapes
| selected' = selected
|__________________________________________________________________________
EXERCISE 17.3
In Section 17.2.5, we said
that the specification Algebraic-draw could be extended
to say that a move, resize or unselect after a delete
has no effect. The axiom for unselect looks like this:
(9) unselect(delete(g))
= delete(g)
Write two more axioms (10) and (11) which say the
same about move and resize. Now use axioms (4) and
(5) to show that (9) implies both your new axioms.
answer
The three additional axioms are:
(9) unselect(delete(st))
= delete(st)
(10) move(p,delete(st))
= delete(st)
(11) resize(p,delete(st))
= delete(st)
Axioms 4 and 5 are:
(4) move(p,unselect(st))
= unselect(g)
(5) resize(p,unselect(st))
= unselect(g)
To show that Axiom 10 is derivable from Axioms 4
and 9 we can argue as follows:
| move(p,delete(st)) |
|
= move(p,unselect(delete(st)) |
|
by Axiom 9 |
|
= unselect(delete(st)) |
|
by Axiom 4 |
|
= delete(st) |
|
by Axiom 9 |
A similar argument shows that Axiom 11 is derivable
from Axioms 5 and 9.
EXERCISE 17.4
Imagine a normal calculator
except that it displays A for 0, B for 1, up to J for 9.
So the number 372 would appear as DHC. Does this affect
the formal transparency of the calculator? Should it?
answer
Formally, this would not affect the transparency
property of a calculator. Any function from display
to effect that held for the numbers would also hold
for their alphabetic counterparts by just composing
it with the code A for 0, B for 1, up to J for 9.
Of course, most people would probably find the encoded
calculator quite a bit more difficult to use than
one that used the normal ten digits. The important
lesson here is that the formal expression of the transparency
property does not indicate how difficult it is for
a human to determine the function between display
and effect. The formal expression just requires that
there be some function. In practice, human users would
probably judge the encoded calculator as unpredictable
(that is, not transparent). The moral is that even
though we can capture a usability property formally
this does not mean that we have captured the entire
intent of the property. The transparency property
would have to be augmented in order to measure the
complexity, from the user's perspective, of the function
between display and effect.
EXERCISE 17.5
To some extent undo is similar
to the 'back' command or button found in many web browsers,
help systems and hypertext systems. Is the 'back' button
on a browser just like undo? Hint: consider scenarios
where the pages are web forms updating a database
answer available for tutors only
EXERCISE 17.6
Experiment with the 'back'
button on different browsers, help systems, etc. Record
systematically the behaviour as you visit pages and
use the 'back' button, and try to build a model (informal
or formal) of the system. Pay particular attention to
what happens if you revisit the same page during the
same 'drill down' and the behaviour in systems with
multiple windows/frames. (Note that this behaviour does
differ dramatically even between different versions
of the same web browser.)
answer available for tutors only
EXERCISE 17.7
Sections 17.2.1 and 17.2.2
give two reasons for using formal methods in HCI: communication
and analysis. These are focused on the sort of mathematical
models found in chapter 17. However, there are other
sort of 'formal' modelling in HCI: dialog notations
are formal models of the syntax of the humancomputer
conversation, hierarchical task analysis is a formalisation
of the task structure, some cognitive models are effectively
formal models of the user's mind.
- Are communication
and analysis reasons for using these other sorts of
formalism?
- Can you think of other reasons why you
would or would not use formalisms?
- Try to use these
pros and cons to formulate issues in the choice of appropriate
forms of formal model and analysis.
answer available for tutors only
EXERCISE 17.8
This exercise is based on the mobile
phone scenario on the book website at: www.hcibook.com/e3/scenario/phone/.
List the main elements of the state of
the phone (you can use programming language variable
declarations for this) and then write down a step-by-step
walkthrough of the state as the user accesses a shortcut
at position '3' as in steps C.1C.10 of scenario C.
answer available for tutors only
EXERCISE 17.9
This exercise is based on the nuclear
reactor scenario on the web at: www.hcibook.com/e3/scenario/nuclear/.
You will need to refer to this while completing the
exercise.
The exercise is in four parts, but you
will probably find it easier to work on them in parallel.
As you try to define actions you will find state elements
you have missed and as you work through the scenarios
you will probably find problems that you need to go
back and change in the state and actions.
(a) Complete the following partial description
of the state of the nuclear control panel.
________________________________________________________________
| Alarm_State: {Green, Amber, TempRed, Red}
| Confirm_Needed: Boolean [ that is true or false]
| Target_Pressure: Nat [ that is { 0, 1, 2, … } ]
| Target_Temp: Nat
| Target_Flow: Nat
| Manual_Override_Value: Nat
| ...
________________________________________________________________
(b) Here is a description of the state
change for two actions: when a digit is pressed on
the keypad and when the '-' key is pressed.
Note we have not written it in 'proper' Z, but in
a form of pseudo code.
keypad_digit(d)
________________________________________________________________
| add d to the right-hand end of Manual_Override_Value
________________________________________________________________
alarm_lower [minus key is pressed]
________________________________________________________________
| if ( Alarm_State is Red or Alarm State is TempRed )
| then set Alarm_State to Amber
| if ( Alarm_State is Amber or Alarm_State is Green )
| then set Alarm_State to Green
________________________________________________________________
Using these to guide you, complete the
following two partial descriptions of the state changes
for the CONFIRM and CANCEL buttons on the Emergency
Confirm control panel
confirm
________________________________________________________________
| set Confirm_Needed to false
| if ( Alarm_State is TempRed )
| then set Alarm_State to Red
| ... something about emergency shutdown too
| ...
________________________________________________________________
cancel
________________________________________________________________
set Confirm_Needed to false
| if ( Alarm_State is TempRed )
| then set Alarm_State to Amber
| ... something about emergency shutdown too
| ...
________________________________________________________________
(c) Produce descriptions of the state
change for the following actions:
(i) alarm_higher
- the '+' key is pressed on the Alarm Control panel
(ii) shutdown -
the IMMEDIATE SHUTDOWN COMMENCE button has been pressed
on the Emergency Shutdown panel
(iii) select_target(targ)
- the target pulldown has been used on theManual Override
panel. targ is one of
{Pressure, Temp, Flow}
(iv) set_target_value
- the SET button has been pressed on the Manual Override
panel
(d) Check your state and actions by running
through the scenario and annotating each action with
the current state. Use the following example of the
first few steps as a guide to the appropriate level
of detail.
| Initial state: | Alarm_State
is Green |
| Confirm_Needed is false |
| etc. ... |
| Steps 1, 2 | no system actions |
| Step 3 | press '+' twice- alarm_higher:
- Alarm_State = Amber
- alarm_higher:
- Alarm_State = TempRed
Confirm_Needed = True
|
| Step 4 | button glows because Confirm_Needed = True |
| Step 5 | no system action |
| etc | |
answer available for tutors only
 |
A two-function calculator has the following
buttons 0-9, +, - and =. These would comprise the
command set (C) of a PIE model of the calculator.
The state (E) would consist of three components: the
two current number being entered, the last number
(to be operated on) and the pending operation (+ or
-). The display (D) is simply a signed number. For
this example, ignore the result.
Write down (semi-formally) the doit function
updating the state for each user command and the display
function relating the state (E) to the current display
(D). To check your definitions: what does the display
have on it after the user has entered '2 + 3 +'? Most
calculators would show 5, does yours?
Consider the displays after the sequences
'2 + 2' '2 +' and the effect on each of the additional
user input of 3. Does the calculator satisfy the transparency
property? [page 614] |
 |
|





